Insert Interval

Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).

You may assume that the intervals were initially sorted according to their start times.

Example 1:
Given intervals [1,3],[6,9], insert and merge [2,5] in as [1,5],[6,9].

Example 2:
Given [1,2],[3,5],[6,7],[8,10],[12,16], insert and merge [4,9] in as [1,2],[3,10],[12,16].

This is because the new interval [4,9] overlaps with [3,5],[6,7],[8,10].

10/7/2015 update

Insert the newInterval to the original interval vector, and copy the algorithm in the Merge Interval question.

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Solution {
public:
    vector<Interval> insert(vector<Interval>& intervals, Interval newInterval) {
        vector<Interval> ans;
        intervals.push_back(newInterval);
        sort(intervals.begin(), intervals.end(), [](Interval a, Interval b){
           return a.start < b.start; 
        });
        Interval it;
        bool valid = false;
        for(auto interval : intervals){
            if(valid == false){
                it = interval;
                valid = true;
            }
            else{
                if(interval.start <= it.end){
                    it.end = max(it.end, interval.end);
                }
                else{
                    ans.push_back(it);
                    it = interval;
                }
            }
        }
        if(valid == true) ans.push_back(it);
        return ans;
    }
};

区域覆盖问题。

二分查找找到应该覆盖的pos。然后向后扩展覆盖原来的interval。

很奇怪，目测是o(n)的复杂度，但却超时了。

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Solution {
public:
    vector<Interval> insert(vector<Interval> &intervals, Interval newInterval) {
        if(intervals.empty() || newInterval.start > (*(intervals.end() - 1)).end){//empty or bigger than last element, push it!
            intervals.push_back(newInterval);
        }
        else if(newInterval.end < intervals[0].start){//newInterval is smaller than the first element
            intervals.insert(intervals.begin(), newInterval);
        }
        else{//find the proper position to insert
            int pos = find(intervals, newInterval.start, 0, intervals.size());
            //intervals[pos].start <= netInterval.start, and intervals[pos] is the last element whose start < newInterval.start
            if(intervals[pos].end >= newInterval.start){//overlap with pos
                vector<Interval>::iterator it = intervals.begin();
                int right = newInterval.end;
                while((it + pos + 1) != intervals.end() && (*(it + pos + 1)).start <= right){
                    right = max(right, (*(it + pos + 1)).end);
                    intervals.erase(it + pos + 1);
                }
                intervals[pos].end = max(right, intervals[pos].end);
                //pos may be 0, it may new.start < pos.start 
                intervals[pos].start = min(intervals[pos].start, newInterval.start);
            }
            else{//not overlap with pos
                vector<Interval>::iterator it = intervals.begin();
                int right = newInterval.end;
                while((it + pos + 1) != intervals.end() && (*(it + pos + 1)).start <= right){
                    right = max(right, (*(it + pos + 1)).end);
                    intervals.erase(it + pos + 1);
                }
                newInterval.end = right;
                intervals.insert(it + pos + 1, newInterval);
            }
        }
        return intervals;
    }
    //[start, end)
    int find(vector<Interval> &intervals, int val, int start, int end){
        if(end - start == 1){
            return start;
        }
        int mid = (start + end) / 2;
        if(intervals[mid].start <= val){
            return find(intervals, val, mid, end);
        }
        else{
            return find(intervals, val, start, mid);
        }
    }
};

更新：

遍历整个intervals，对于newInterval，有如下几种情况：

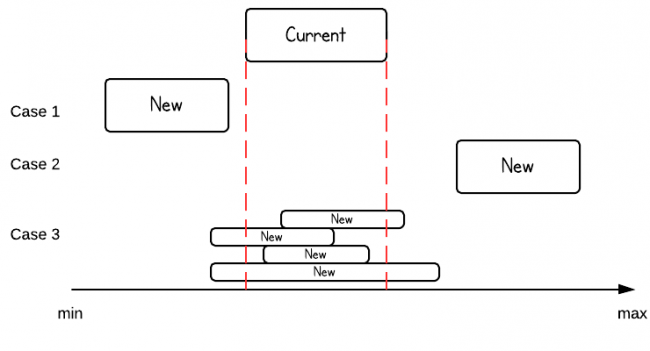
分情况处理，o(n)复杂度，依旧超时。

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Solution {
public:
    vector<Interval> insert(vector<Interval> &intervals, Interval newInterval) {
        for(vector<Interval>::iterator it = intervals.begin(); it != intervals.end(); it++){
            if(newInterval.start > (*it).end){
                continue;
            }
            else if(newInterval.end < (*it).start){
                intervals.insert(it, newInterval);
                return intervals;
            }
            else{
                newInterval.start = min(newInterval.start, (*it).start);
                newInterval.end = max(newInterval.end, (*it).end);
                intervals.erase(it);
                it--;
            }
        }
        intervals.push_back(newInterval);
        return intervals;
    }
};